Gradients are not explanations
Gradient-based explanation methods are often perceived as the gold standard in machine learning interpretability. The authors of “Attention is not Explanation” used input gradients as the ground truth. They argued that attention isn't an explanation because it correlates poorly with gradients. This paper from Google Research argued that there are no compelling reasons to use attention when we can use gradient-based explanations.
However, my recent research has led me to question this assumption. In An Unsupervised Approach to Achieve Supervised-Level Explainability in Healthcare Records, we compared a wide range of explanation methods. To my surprise, gradient-based explanation methods produced the worst explanations—even worse than attention. In this blog post, I will try to explain why.
By the end, I hope to convince you that gradient-based explanation methods, such as InputXGradients and Integrated Gradients, are far from being a gold standard—they barely qualify as a rusty iron standard. Let's dive in!
Gradient-based explanations 101
Gradient-based explanation methods produce explanations using the output gradients with respect to the input features. For deep neural networks, they are typically calculated using backpropagation. While gradients can be challenging to grasp intuitively, especially in the context of deep neural networks, I find the following explanation helpful:
Think of the output gradient with respect to an input feature as how much the output wiggles if you slightly wiggle that input feature. We're talking about an infinitesimally small input wiggling—so small it's almost undetectable.
These methods measure the importance of each input feature by calculating how much the output changes when each feature is wiggled separately. This results in a score per feature representing its importance to the output, a form of explanation known as feature attribution.
Let's look at a concrete example to better understand how gradient-based explanations work. Consider the following linear model:
For this model, we calculate the input gradient as follows:
As you can see, the input gradients of a linear model are simply its weights. At first glance, this might seem like a good estimation of each feature's contribution. However, there's a significant issue: this explanation is unaffected by the actual input values.
For instance, given an input (0.3, 0, 0.6, 0.1), the contribution of the second feature should be 0, not 0.5. This is where a method called InputXGradient comes in. It addresses this limitation by multiplying the input and the input gradients:
Using our example input (0.3, 0, 0.6, 0.1), we get (0.03, 0.00, 0.12, 0.02). This explanation more accurately reflects each feature's contribution to the output, taking into account both the model's weights and the specific input values.
This example demonstrates how gradient-based methods attempt to provide meaningful explanations for model predictions. However, as we'll explore in the next section, these methods have significant weaknesses that limit their effectiveness as explanatory tools.
Their weaknesses
Non-linear functions
Above, I showed you that InputXGradient works well for linear models. However, deep neural networks are rarely linear; that’s the whole point of using them. Unfortunately, gradient-based explanation methods often fail when dealing with non-linearity. Let's look at a simple demonstration.
Take the following model:
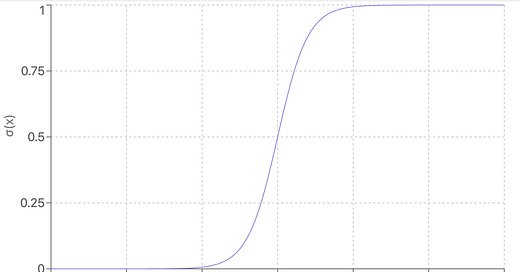
This model takes two input features. It uses a sigmoid function (σ) that takes the second feature as input. A sigmoid function is a non-linear function and looks like this:
Now, let’s say we provide the model with input (10, 10). We then get the following output:
In blue, you can see the contributions from each feature. You can clearly see that the second feature is far more influential than the first. So, which features are important according to InputXGrad?
According to InputXGrad, the second feature is unimportant, which is clearly wrong. So why does this happen? If you look at the plot for large values, wiggling the input of a sigmoid function has little impact on the output—the line is flat.
This example illustrates how gradient-based explanation methods struggle with non-linearities, which are fundamental to the activation functions in deep neural networks. However, while basic gradient methods struggle with non-linearity, more advanced techniques have been developed to address this issue. One such method is Integrated Gradients. Let's explore how it works.
How Integrated Gradients deals with non-linearity
Integrated Gradients requires the user to define a baseline value representing an uninformative input. In image classification, this can be an all-black image or an image of white noise. Mask tokens are commonly used in text classification.
Imagine a straight line between the input and the baseline value. Integrated Gradients takes small steps along this line. At each step, it calculates the gradients. It then averages the gradients across all steps. Finally, it multiplies this average by the difference between the input and baseline values.
Let’s consider the previous example. We use a baseline value of (0,0) and a step size of 50. Imagine a straight line between (0,0) and (10,10). We take 50 steps along this line and calculate the gradient at each step. We average the gradients and get (0.01, 0.98). We then multiply it with the input minus the baseline values.
So (0.1, 9.8) is our final explanation. This is much better! It correctly identifies that the second feature is more important than the first, aligning with our intuitive understanding of the model.
It is currently unclear to me whether Integrated Gradients solves the non-linearity issue and exactly why. I can see that it works for toy examples, but I am unsure how it works for real data. In my two explainability papers, Integrated Gradients perform similarly to InputXGradients, which could suggest it doesn’t solve the issue in all scenarios.
Even if Integrated Gradients solves the non-linearity problem, it's important to note that they don't solve all the problems associated with gradient-based explanations. There are still other issues to consider, which we'll explore in the next section.
What does wiggling the input even mean?
While it's easy to imagine wiggling input features in our simple numerical examples, the concept becomes much more complex and abstract for real-world tasks, especially in text classification.
The weirdness of word gradients
Consider an email spam classification task. The model takes an email as input and outputs a score representing the probability of the email being spam. In this context, what does wiggling the input mean? How do we wiggle words?
Most text classification models represent each word or sub-word as a vector. You can think of these vectors as points in a high-dimensional space. For example:
When we calculate gradients for these word vectors, we get a vector per word, not just a single number. This gradient vector points in the direction of maximum impact on the output, and its size indicates the magnitude of that impact. Researchers typically use this size to estimate a word's importance.
But here's where things get weird:
Interpretation Challenges: How do we make sense of directions in this word space? What does it mean to move a word towards "computer" or away from "fruit"?
Semantic Discontinuity: Small changes in this continuous space might lead to nonsensical "words.” What meaning does the midpoint between "computer" and "fruit" have?
These issues reveal a fundamental mismatch: We're using continuous mathematics to explain discrete, semantic concepts. The result? Gradient-based explanations often lack clear linguistic meaning.
Let’s be clear: they accurately measure how tiny changes to the input change the output; I just don’t think it’s aligned with how people interpret the explanations.
Can Integrated Gradients save the day?
Spoiler alert: No, they can't. Let's see why.
Consider this visualization:
This simplified 2D space shows words as points, with the red line representing the path between a baseline (<mask>) and the word "cat" in Integrated Gradients.
This method introduces new problems:
Meaningless Intermediates: The path between <mask> and "cat" passes through non-existent words. What do these points mean?
Arbitrary Baselines: Why choose <mask> as the baseline? How would using "animal" or "dog" change our explanation?
Edit
I’ve realized that passing through nonsensical representations may not be an issue. However, I’ve found another issue with integrated gradients that causes it to struggle with architectures such as transformers. I haven’t decided whether to publish my new findings as a blog post or paper.
Wrapping up
Throughout this discussion, we've focused on two primary weaknesses of gradient-based explanation methods:
Struggle with Non-linearity: Basic gradient methods often fail when dealing with non-linear functions, which are ubiquitous in modern machine learning models.
Difficult to interpret: In the realm of text classification, gradients - whether basic or integrated - prove to be unintuitive and challenging to interpret. I don’t think “how much the output wiggles when wiggling an input feature” is how most people interpret an explanation.
While we focused primarily on text classification, these interpretability issues likely extend to other domains as well. Even in image classification, where gradients might seem more intuitive, the fundamental challenge of translating mathematical operations into human-understandable explanations persists. For example, what does it mean if the output changes because a pixel becomes slightly darker?
So, what are the alternatives to gradient-based methods? I think for inputs with few features, perturbation-based explanation methods, such as LIME or SHAP, are excellent choices. Attention sometimes works well, and sometimes don’t. It depends on your model. If you use transformers, transformer-specific explanation methods, such as DecompX or ALTI, are good choices. I’ve found DecompX to work better than ALTI. However, DecompX uses a lot of memory for long inputs, so that may be a deal-breaker. I’m currently working on a way to fix this, so hopefully, I will have a good explanation method in a short time!
I’ll wrap up here. Do you agree with my points or think I’m off base? I’d love to hear your thoughts!